タイプ14-2
b=30 c=a+30、d=90-1/2aのとき f=1/2a
証明
番号
141 a=20 b=30 c=50 d=80 f=10
270 a=40 b=30 c=70 d=70 f=20
2通りの三角形が解決します。
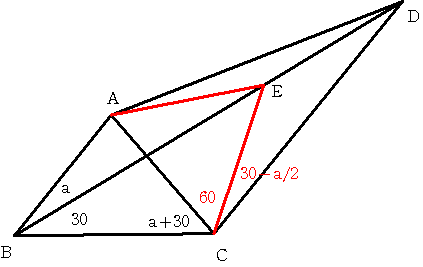
角CAE=60度となる点EをBD上に取ると
角AEP+角EAP=角PBC+角PCBから 角AEP=a
すると三角形ABEは二等辺三角形となるから AB=AE
三角形ABCは二等辺三角形であるから AB=AC
よって AE=ACとなり 三角形ACEは正三角形である。
一方 三角形CEDにおいて 角BEC=60-a=2×角ECD
よって三角形CEDは二等辺三角形であるから EC=ED
よって AE=EDとなり 角AEP=aより 角ADE=a/2となる