タイプ13
a=30 c=3b-90 d=90-b、のとき f=2b-60
補題
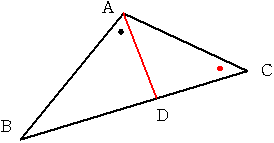
三角形ABCの辺BC上に点Dをとる。角BAD+角ACD=90度のとき
外心は直線AD上にある
補題の証明
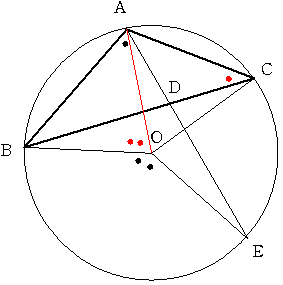
外心をOとするADの延長と円の交点をEとする
中心角と円周角の関係より
角BOE=2×角BAD
角AOB=2×角ACB
辺々たすと 条件より 角AOE=180度
よって A,O,Eは同一直線上にあり
Oは 直線AD上にあることがわかる
証明
a=30 c=3b-90 d=90-b、のとき f=2b-60
a=30 b=40 c=30 d=50のとき f=20 219番
a=30 b=50 c=60 d=40のとき f=40 233番
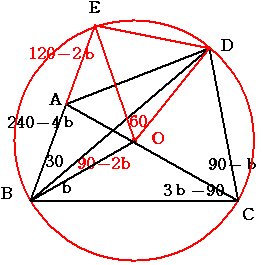
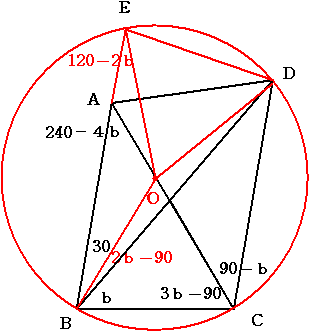
角DBC+角ACD=90度 より 補題からAC上に三角形ABCの外心が存在する
外心をOとすると
角DBO=絶対値(90-2b) OがBDの上にある場合と下にある場合があるがどちらにしても
角OEB=角OBE=120-2b 一方 角BAC=240-4bより 角AOE=120-2b
よって 三角形OAEは二等辺三角形となり AO=AE .....①
角EOD=2×角EBD=60度であるから三角形ODEは正三角形 よって OD=DE ......②
三角形ADEと三角形ADOは①②より合同
よって 角ADO=30度
いずれの図も 角ADB=120-2b となる