タイプ12
b=a c=60-a、d=60-aのとき f=30
a=10 のとき
a=b=10 c=d=50 f=30
a=20 のとき
a=b=20 c=d=40 f=30
a=30 のとき
a=b=30 c=d=30 f=30 これはタイプ1
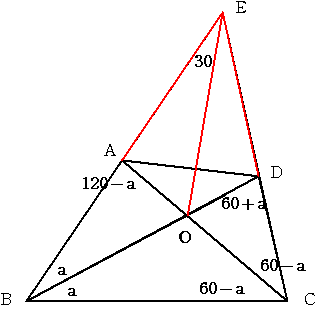
ABとCDを延長し交点をEとします。
三角形EBCにおいて BD および CAは角の二等分線になっているのでその交点
Oは内心です。
よって 角AEO=90-a-(60-a) =30
Langleyの問題
タイプ12
b=a c=60-a、d=60-aのとき f=30

a=10 のとき
a=b=10 c=d=50 f=30
a=20 のとき
a=b=20 c=d=40 f=30
a=30 のとき
a=b=30 c=d=30 f=30 これはタイプ1
ABとCDを延長し交点をEとします。
三角形EBCにおいて BD および CAは角の二等分線になっているのでその交点
Oは内心です。
よって 角AEO=90-a-(60-a) =30
一方 角BAC+角CDB=(120-a)+(60+a)=180
よって四角形AODEは円に内接する
以上から 角ADB=角AEO=30度となる