タイプ11
c=90-a、d=2aのとき f=90-a-b
補題
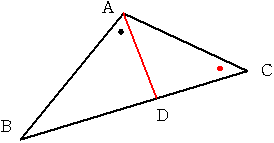
三角形ABCの辺BC上に点Dをとる。角BAD+角ACD=90度のとき
外心は直線AD上にある
補題の証明
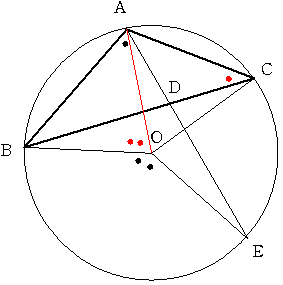
外心をOとするADの延長と円の交点をEとする
中心角と円周角の関係より
角BOE=2×角BAD
角AOB=2×角ACB
辺々たすと 条件より 角AOE=180度
よって A,O,Eは同一直線上にあり
Oは 直線AD上にあることがわかる
証明
c=90-a、d=2aのとき f=90-a-b
番号
12 41 62 74 81 85 91
102 124 143 156 163 170 183
202 214 224 234 246 256 267 278 287 292 298
308 314 326
28通りの三角形が解決します。
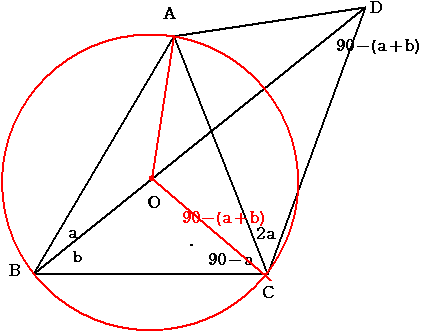
角ABD+角ACB=90度 より 補題からBC上に三角形ABCの外心が存在する
外心をOとすると
角AOC=2(a+b)
角ACO=(180-2(a+b))÷2=90-a-b
角BDC=90-(a+b)であるから
四角形AOCDは円に内接する
よって 角ADB=角ACO=90-(a+b)