タイプ11-3
b=30-a、c=90-a d=4a のとき f=30
証明
a=10のとき
a=10 b=20 c=80 d=40 f=30 42番の証明
a=20のとき
a=20 b=10 c=70 d=80 f=30 104番の証明
2通りの三角形が解決します。
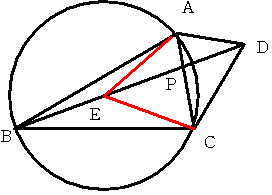
角ABD+角ACB=90度 より タイプ11の補題からBD上に三角形ABCの外心が存在する
外心をEとすると
角AEC=2(a+b)=60度 よって 三角形AECは正三角形となる。
このとき 角BDC=180-(b+c+d)=60-2a 角CED=2b=60-2aであるから
三角形CDEは二等辺三角形となる よって CD=CE=CA より
三角形ACDも二等辺三角形であり 角CDA=(180-d)/2=90-2a
角ADB=角CDA-角CDE=(90-2a)-(60-2a)=30