タイプ10
b=3a、c=90-2a、d=30のとき f=30 (0<a<45)
補題
ひとつの角とそれに隣り合う1つの辺 及びその角に隣り合わない辺の長さが与えられているとき
考えられる三角形は2種類で そのうち1つの角は互いに補角となっている。
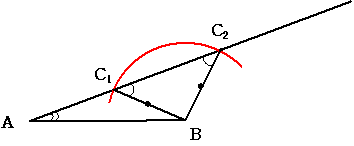
角AとAB BCの長さ が与えられているとします
条件を満たす3角形を描くとします。 長さABを確定し BAから与えられた角をもつ 半直線mを描きます
次にBを中心として半径BCで円を描くと mとの交点はたかだか2つでその点を C1 C2
とすると 3角形ABC1 および3角形ABC2 のみ が 条件を満たす三角形として得られます。
3角形AC1C2は二等辺3角形ですから このような条件を満たす3角形の角AC1Bと 角AC2Bは互いに等しいか
補角をなしていることがわかります。
証明 b=3a、c=90-2a、d=30のとき f=30 (0<a<45)
 a=10のとき
a=10のときa=10 b=30 c=70 d=30 f=30 88番の証明
a=20のとき
a=20 b=60 c=50 d=30 f=30 167番の証明(別解)
a=30のとき
a=30 b=90 c=30 d=30 f=30 タイプ1になる
a=40のとき
a=40 b=120 c=10 d=30 f=30 195番の証明
ただし左右対称なので 195の条件では100度となる
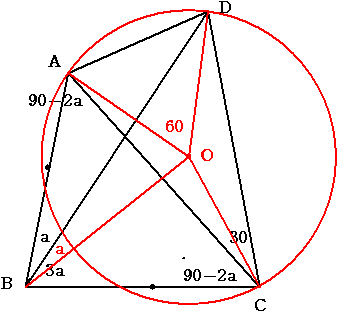
角BAC=180-(a+3a)-(90-2a)=90-2aより3角形ABCは二等辺3角形
よって AB=CB
このとき 3角形ACDの外接円の中心をOとすると
三角形AOBと3角形COBは合同 (OA=OC AB=CB OB共通)
よって 角OBD=(a+3a)/2-a=a
角ACD=30°より 角AOD=60° よって3角形OADは正三角形
よって OD=AD
ここで 3角形ABDと3角形OBDは合同
(BDは共通 角ABD=角OBD AD=OD
補題よりこのような3角形は2通り考えられるが
角BAD+角BOD=360-(2a+60)=300-2a>210となり互い補角にはならない
よって合同となる)