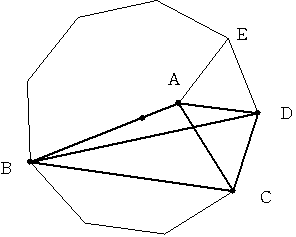
Langleyの問題　　36

a＝10°　ｂ＝20°　c=50°　ｄ＝50°　　答20°

上の図のように正9角形を描き　この内部に三角形ADEが正三角形になるように
点Aをとります。
正9角形の内角のひとつは　180-360/9=140°となっています。

CDに対する中心角は　360/9＝40°
CDに対する円周角DCB=40/2=20°　つまり　b=20°であることが確認できます。

BCに対する中心角は　40×３=120°(CDに対する中心角３つ分）ですから　角OBC=(180-120)/2=30°
よって　a=30-20=10°であることが確認できます。

三角形ADCはAD=CDの二等辺三角形で　角ADC=140-60=80であるから
d=(180-80)/2=50°になります。

CDに対する円周角BCD(鈍角BCDの方）はCD５つ分なので　20×5=100°
よってc=100-d=50°になります　

つまり上のようにつくった四角形ABCDは条件を満たしていることがわかります。
また逆に条件を満たす４角形は　すべて相似ですからこの四角形について角を
もとめればよいことがわかります。

角BAD=(360-60)/2=150より　角ADB=180-150-10=20°となります