Langleyの問題　　２１９

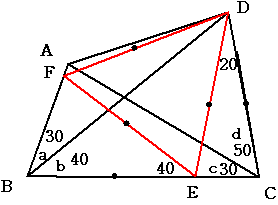
a＝30°　ｂ＝40°　c=30°　ｄ＝50°

辺BC上に角CDE=20度となる点Eをとる。辺AB上（またはABの延長線上）に
角BEF=40度となる点Fをとります。

三角形CDEは80度　20度　80度の二等辺三角形　となるので　DC=DE　　�@

三角形BDEは40度　40度　100度の二等辺三角形　となるので　BE=DE　　　�A

三角形BEFは70度　40度　70度の二等辺三角形　となるので　BE=EF　　　�B

�A�Bより　DE=EF　また　角DEF=60度より　三角形DEFは正三角形

よってDE=DF
これと�@からDC=DF

すると三角形CDFは二等辺三角形であり　角DCF=50度となる
ということは　Fは実はAと一致していることがわかる

よって　角ADB=角FDB=60-40=20度となります