Langley偺栤戣丂丂166
a亖20亱丂倐亖60亱丂c=30亱丂倓亖50亱
夝摎丂晜楺偝傫

崟偄妏偑曗彆慄傪堷偔慜偵寁嶼偱偒傞妏
愒偄妏偑曗彆慄傪堷偄偨偁偲偱寁嶼偱偒傞妏偲側偭偰偄傑偡丅
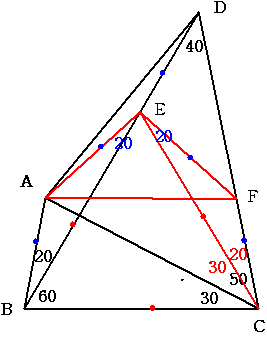
BD忋偵佢BCE=60搙偲側傞揰E傪偲傝傑偡丅
3妏宍BCE偼惓嶰妏宍偲側偭偰偄傑偡丅
BC偵暯峴偱A傪捠傞捈慄偲CD偲偺岎揰傪F偲偟傑偡丅
巐妏宍ABCF偼摍媟戜宍偲側偭偰偄傑偡丅丂AB=FC丂丂...嘆
3妏宍ABC丂偲丂3妏宍AEC丂偼崌摨偱偡偐傜丂AB=AE丂丂...嘇偲側傝傑偡
丂丂乮AC嫟捠丂佢ACB=佢ACE丂BC=EC乯
3妏宍ABE丂偲丂3妏宍FCE偼崌摨偱偡偐傜丂AE=FE丂丂...嘊偲側傝傑偡丅
丂丂乮AB=FC丂佢ABE=佢FCE丂BE=CE)
嘆嘇嘊傛傝丂FC=FE丂傛偭偰丂佢FEB=20搙丂佢BEF=60+20=80亱
傛偭偰佢DFE=80-40亖40搙
偙偺偙偲偐傜丂EF=ED偑傢偐傝傑偡丅
偙傟偲丂嘊偐傜丂AE=ED丂偲側傝丂3妏宍AED偼擇摍曈3妏宍偱
佢AEB=佢CEF=20搙傛傝丂佢ADB=10亱丂傪摼傑偡丅
夝摎丂儕儞僨儞偝傫
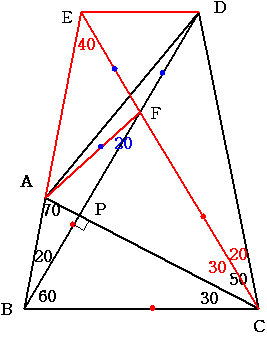
BA偺墑挿慄忋偵丂BC偲ED偑暯峴偲側傞揰E傪偲傝傑偡丅
CE偲BD偺岎揰傪F偲偟傑偡
巐妏宍BDE偼摍媟戜宍偱偡偐傜丂嶰妏宍BCF丂嶰妏宍DEF偼惓嶰妏宍偲側傝
DF=EF偲側偭偰偄傑偡丂丂乧嘆
妏BPC=90搙偱偡偐傜丂嶰妏宍BCP偲FCP偼崌摨偲側傝BP=FP
偙傟傛傝嶰妏宍ABP偲嶰妏宍AFP傕崌摨偲側傝丂妏BAP=妏FAP=70搙偱偁傞偙偲偑傢偐傝傑偡丅
嶰妏宍AEF偵偍偄偰妏AEC=40搙丂妏EAF=180-70亊2=40搙偲側傝傑偡偐傜
嶰妏宍AFE偼擇摍曈嶰妏宍偱丂EF=AF丂
偙傟偲丂嘆偵傛傝丂AF=EF丂傛偭偰嶰妏宍AFD偼擇摍曈嶰妏宍偲側偭偰偄傞偙偲偑傢偐傝傑偡丅
妏AFP=妏ABP=20亱傛傝丂妏ADF=10搙偲側傝傑偡丅