Langleyの問題　　151

a＝20°　ｂ＝40°　c=40°　ｄ＝30°

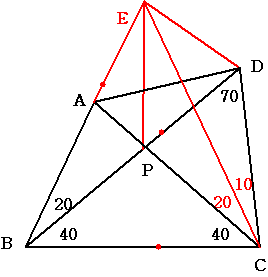
ABの延長線上に　角BCE=60度となる点Eを取ります。
三角形BCEは正三角形となっています。　BC=CE　…�@

三角形BCDも底角70度の二等辺三角形になっていますから　BC=BDとなります。
これと�@より　BE=BDとなり　三角形BDEが二等辺三角形となります。

角BED=(180-20)/2=80であり　角APD=角BPC=180-(40+40)=100ですから
四角形APDEは円に内接しています。

明らかにEPは三角形BCEで角BECの二等分線ですから　角AEP=30°
よって角ADP=30°となります。