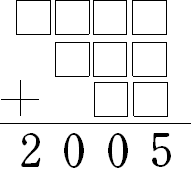
上の四角の中に0から9までの数を1つづつ入れて和が2005になるようにします。
ただし同じ数は2回使えません。うまく数字が入る答は168通りあります。
四角は9個なので数字は1つあまりますが、式を完成させたときに どんなときも必ず
使われる数字をすべて足すといくらでしょうか。
解答はメールか、フォームをクリックして送信してください。
120000アクセス記念問題 (2月8日〜)
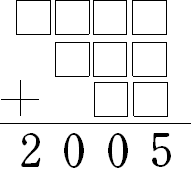
上の四角の中に0から9までの数を1つづつ入れて和が2005になるようにします。
ただし同じ数は2回使えません。うまく数字が入る答は168通りあります。
四角は9個なので数字は1つあまりますが、式を完成させたときに どんなときも必ず
使われる数字をすべて足すといくらでしょうか。
解答はメールか、フォームをクリックして送信してください。
解答1なかさん
十進数とその各位の和を9で割った余りは等しい。2005を9で割った余
りは7なので、□9個の和を9で割った余りも7である。一方、数字10個全
部足すと45と9で割り切れる。したがって、異なる数字9個の和を9で割っ
た余りが7になるためには、「2」を余すしかない。つまり、□9個の和は、
45−2=43である。
解答2
明らかに4桁の数の1000の位の数は1です
1の位の合計は 5または15または25です。
1の位の最低の和は 0+2+3=5で 最高の和は 9+8+7=24ですから1の位の数は5または15
1の位の和が5のとき
10の位の数の和は10または20
10の位の数の和が10のとき 100の位の数の和は9
このとき各位の数の総和は 5+10+9+1=25 で 1から9までの和が45であるから1つを除いて25にはならない
10の位の数の和が20のとき 100の位の数の和は8
このとき各位の数の総和は 5+20+8+1=34で1から9までの和が45であるから1つを除いて25にはならない
よって 1の位の合計は15になっています
10の位の合計は (1の位から1あがってくることを考えて) 9または 19です(3つの数の和は1の位で考えたように9から24の間です)
その1 10の位の和が9のとき
100の位の和は(10の位の数から 1上がってくることを考えて)9です。
すると 各位の数の和は 1の位15 10の位 9 100の位 9 1000の位 1 であり
すべての数を足すと 15+9+9+1=34です
ところが 1から9までの数の和が45ですから どの数を除いても34にはなりません
その2 10の位の和が19のとき
100の位の和は(10の位の数から 2上がってくることを考えて)8です。
すると 各位の数の和は 1の位15 10の位 19 100の位 8 1000の位 1 であり
すべての数を足すと 15+19+8+1=43です
ところが 1から9までの数の和が45ですから 使われない数は 2であることがわかります。
実際 4桁の数の最小は 1034で 1034+875+96=2005のように2が使われない解答がありますから 答は2のみなのです。
(4桁の最大の数は1598となっています。)
以上から 2を除く数字が常につかわれていることがわかり 必ず使う数の和は 45-2=43となります。(1から9までの和は45ですから)