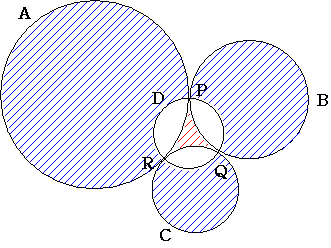
��̐}�̂悤�ɔ��a���Ucm�̉~A�@���a���Scm�̉~B�@���a��2cm�̉~C���݂��ɊO�ڂ��Ă��܂��B
�~A�Ɖ~B�̐ړ_��P�@�~B�Ɖ~C�̐ړ_��Q�@�~C�Ɖ~A�̐ړ_��R�Ƃ��܂��B
�_P,Q,R��ʂ�~��D��`���܂��B
�}�̐Ԃ̎ΐ������̖ʐςƁ@�̎ΐ������̖ʐς����͂�����ɂȂ�ł��傤���B
��
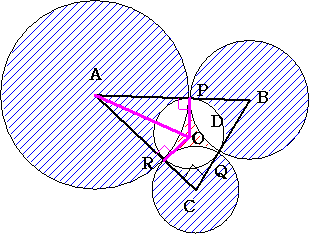
�~A�̒��S��_A�Ƃ��܂��i���������ł��������Ȃ��Ǝv���܂��j
�~A�̓_P�ł̐ڐ��Ɓ@�_R�ł̐ڐ��̌�_��O�Ƃ��܂��B
�O�p�`APO�ƎO�p�`ARO�͍����ł�����@OP=OR
�~B�ł����l�ɍl����Ɓ@OP=OQ
����ā@O�͉~D�̒��S�ł��邱�Ƃ��킩��܂��B�i���́@�O�p�`ABC�̓��S�ɂȂ��Ă��܂��j
�@
�O�p�`ABC�́@AB=10cm�@BC=6cm�@CA=8cm�ł�����
�R�F�S�F�T�̒��p�O�p�`�Ł@���̖ʐς́@1/2�~6�~8=24cm^2�ƂȂ�܂��B
�~D�̔��a��a�Ƃ���Ɓ@�O�p�`ABC�̖ʐς�
�@�O�p�`ABO+�O�p�`BCO+�O�p�`CAO
=1/2�~(AB+BC+CA)�~a=1/2�~24a=12a�@cm^2�ł�����@a=2�ł��邱�Ƃ��킩��܂��B
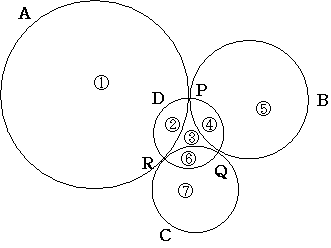
�~�ŋ����ʐς���̂悤�ɖ��O�����܂�
���߂鍷��
�@+�D+�F-�B�ƂȂ��Ă��܂�����������̂悤�ɓǂݑւ��Ă����܂�
�@+�D+�F-�B=(�@+�A+�C+�D+�E+�F)-(�A+�C+�E+�B)
�@�@�@�@�@�@�@�@�@=�~A+�~B+�~C-�~D
�@�@�@�@�@�@�@�@�@=�~A+�~B
����Ėʐς̍��́@A+B=36�~3.14�{16�~3.14=52�~3.14=163.28�@
���̖��쐬�̂��ƂɂȂ����̂�
http://ha3.seikyou.ne.jp/home/okabayashi/sansu/J/J-a22.htm
�ł��B
CD����̂��̖��������Ƃ��ɍ쐬���܂����B
���̂Ƃ��@C-D����Ɂ@�R�F�S�F�T�̎O�p�`�̒̎d�����������낢�̂�
�����@�����ł������Ă�낤�Ƃ������̂��o���Ă���ł��傤���B�i*^_^*�j