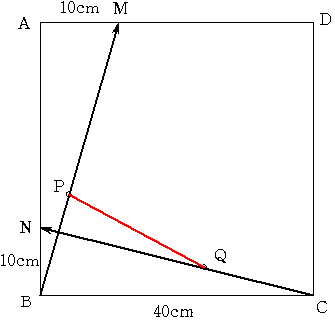
上の図のように一辺が40cmの正方形ABCDの辺AB,AD上に
BN=10cm AM=10cmとなるように点N,Mをとります。
点P.Qは頂点B,Cを出発して 線分BM,CN上をB→M C→Nの
方向へ同じ速さで進みます。
PQの長さが最小になるとき 比BP:PM はいくらになるでしょうか
解答
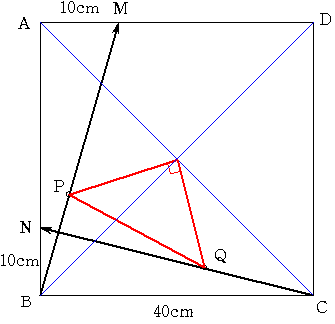
この正方形の対角線の交点をOとし 三角形OPQを考えます。
すると 点B,P,MをOを中心に90度回転した点が 点C,Q,Mとなっていますから
三角形OPQは二等辺三角形となっていることがわかります。
つまりPQが最小である条件は OPが最小であればよいことになるわけです。
また OPが最小となる時は BMとOPが垂直に交わっていることになりますから
そのときのPの位置を求めるとよいことになります。
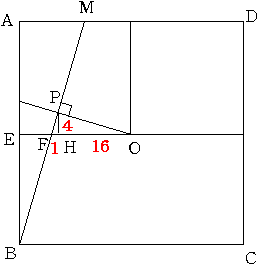
そこで上の図のように点に名前をつけると いたるところに直角をはさむ辺の比が
1:4の直角三角形があることに注意して
FH=1とすると PH=4 OH=16となり OF=17となります
EF=1/2AM=1/4OE ですから EF=1/3OF=17/3
EH=17/3+1=20/3
AM=2EF=17/3×2=34/3
BP:BM=EH:AM=20/3:34/3=10:17
よって BP:PM=10:7