80000アクセス記念問題　（2月14日〜）

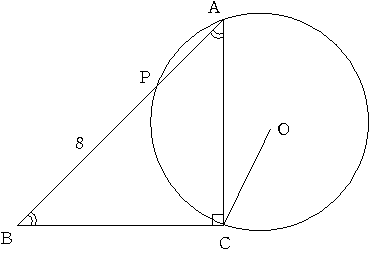
直角二等辺三角形ABCの辺AB上に上のようにBP=8cmとなる点Pをとり
３点A,C,Pを通る円を描いたところ　円の半径OCは5cmになりました。
この時　この直角二等辺三角形の面積を求めてください。（単位は　cm＾2でね^_^;）

解答


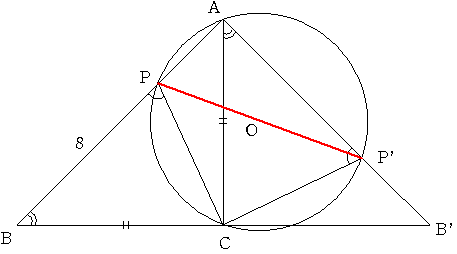
図のように三角形ABCをACを軸として対称移動して　点に名前をつけます。

三角形BCPと三角形ACP'は合同です。
　　辺BC　と辺ACが等しい　（二等辺三角形の仮定より）
　　角PBC　と角P'ACが等しい　（仮定より　45度）
　　角BCPと角ACP'が等しい　（角BPCと角AP'Cが円に内接する四角形の性質から等しくなり
　　　　　　　　　　　　　　　　　　　三角形の残りの角が等しくなる）
よって　AP'=8cmとなります。

次に三角形APP'について考えると　角PAP'=90度ですからPP'=10cmとなります。
なんと　3:4:5の直角三角形になっているではありませんかっ！！

んでAP=6cm
三角形ABB'は1/2×14×14で　三角形ABCの面積はさらにその半分の49cm^2です。