70000アクセス記念問題　（12月12日〜）

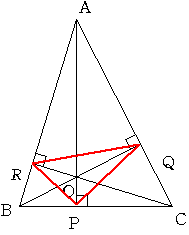
三角形ABCにおいて各頂点から対辺に垂線を下ろすと　３本の線分は１点で交わります（垂心といいます）
それぞれの足を図のようにP,Q,Rとします。
AC=30cm　PC=10cm　角BAC=45度のとき　PQ+QR+RPを求めてください。

　解答


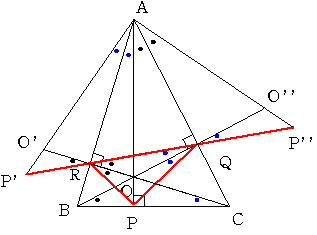
上の図で同じしるしのついてる角度は全部等しいのです。
三角形AOQと三角形BOPにおいて
　角AQO=角BPO=90度
　角AOQ=角BOP　対頂角
よって　角OAQ=角OBP

四角形BPORにおいて　
角BRO=角BPO=90度であるから　BOを直径とする円周上に
点P,Rが乗っかっている。
よって　角OBP=角ORP　（同一円周上の点についての円周角）

四角形AROQにおいて
角ARO=角AQO=90度であるから　AOを直径とする円周上に
点Q,Rが乗っかっている
よって　角OAQ=角ORQ

そこで辺ABに関して三角形APRを対象移動すると
角O'RP'=角ORP=角OQRとなるからP',R,Qは同一直線上にあることがわかる。
また　PR=P'Rであることも明らかである。

同様にPQ=P'Qであるから
PQ+QR+RP=P'P''となる。

そこで三角形AP'P''について考えると
角P'AP''=2×角BAC=90度
辺AP'=AP''=AP=√(30^2-10^2)=20√2の直角二等辺三角形となっているので
P'P''=20√2×√2=40となる。