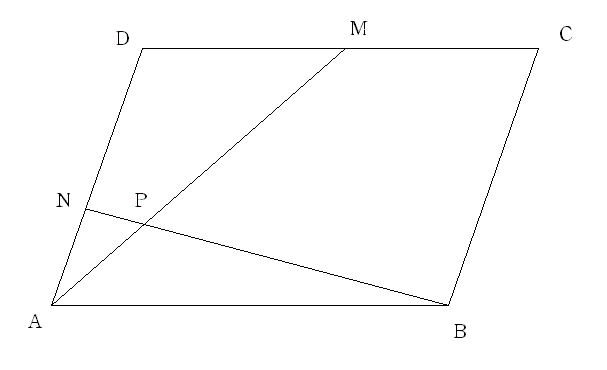
平行四辺形ABCDがあります。辺CDの真ん中の点をM 辺AD上でAN:ND=1:2となる点をNとします。
AMとBNの交点をPとするとき AP:PMを求めてください
50000アクセス記念問題 (6月26日~7月26日)

平行四辺形ABCDがあります。辺CDの真ん中の点をM 辺AD上でAN:ND=1:2となる点をNとします。
AMとBNの交点をPとするとき AP:PMを求めてください
この問題は高校のベクトルの問題でよくお目にかかる問題です。しかし小学生のレベルでとけちゃうんです。
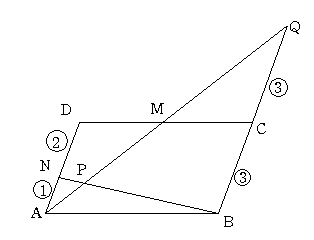
ANの長さを①とします。ND=②となります。
線分AMの延長線と辺BCの延長線の交点をQとします。
三角形ADMと三角形QCMが合同ですからQC=AD=③となります。
また AM:MQ=1:1も成り立ちます。......(A)
次に 三角形APNと三角形QPBが相似で相似比はAN:QB=1:6になりますから
AP:PQ=1:6と成っています。 ......(B)
さて 以上からAQの長さを1として考えると (A)(B)から
AP:PM=AP:(AM-AP)=1/7:(1/2-1/7)=2:5を得ます。