40000アクセス記念問題　（3月22日〜4月22日）

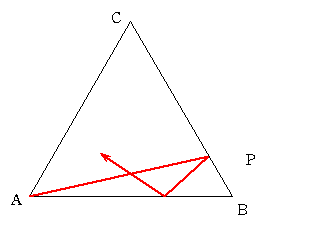
正三角形ABCの内側が鏡のようになっているとします。頂点Aから発した光が辺BC上で反射し、次に辺AB上で反射し、以下同様に
反射を繰り返しある頂点に達しました。ただし　CP:PB=40000:1であるとします。さて、次の問題に答えてください。
（1）反射は辺上で何回起こりましたか　
（2）進んだ距離はAPの長さの何倍ですか
（３）最後にどの点に到達しましたか

正三角形ABCの内側が鏡のようになっている　というのは　辺上で反射するときに　入射角と反射角が等しくなるように
反射する　という意味です

解答

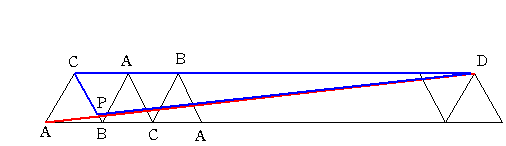
上の図のように正三角形をたくさん並べます。光の反射の時に良くやるように　対称移動した正三角形の内部を光が直進すると
考えるわけです。
CDがABの40000倍になるように並べると三角形ABPと三角形DCPは相似で相似比が40000：1となります。
このことによって　
（2）進む距離は　AP:DP=1:40000であるからAPの4001倍であることがわかります

次に　ADと　各辺の交点の数を求める事によって反射の回数がわかります
左のほうからひっくり返った正三角形CBAと２回交わっています（CBと　BA）
次のひっくり返った正三角形ABCと2回（ACと　CB)
というように40000個のひっくリ返った正三角形と２回づつ交わっていますので40000×2=80000回反射してるようです。
しかし最後のひっくり返った正三角形とは　１回交わり最後の１回はDに到達するので
(1)の解答は　80000-1=79999回　となります。
(
3)最後にDは　A,B,Cのいずれかを決定いたします。
上の図のCDを見てみます　
Cから正三角形の一辺分右の点はAです　
Cから正三角形の二辺分右の点はBです　
Cから正三角形の三辺分右の点はCです
Cから正三角形の四辺分右の点はAです　
Cから正三角形の五辺分右の点はBです　
Cから正三角形の六辺分右の点はCです
…
ということで　一辺の長さの3の倍数辺分右の点はC
　（一辺の長さの3の倍数+1）辺分右の点はA
　（一辺の長さの3の倍数+２）辺分右の点はB
ということがわかり　40000=3×13333+1ですから
Dは実はAであることがわかります。